Decoding the PlayStation 3 Hack: Unraveling the ECDSA Random Generator Flaw

In 2006, Sony unleashed the PlayStation 3, a cutting-edge gaming console that quickly captivated the hearts of millions. However, behind its sleek design and powerful gaming capabilities lay an enticing challenge for hackers. Over the years, a myriad of attempts were made to crack the PS3's defenses, fueled by the desire to run homebrew software and pirate games. Amidst this pursuit, one group of hackers, FailOverflow, embarked on a groundbreaking mission that would send shockwaves through the cybersecurity world.

In December 2010, at the Chaos Computer Congress in Germany, FailOverflow revealed a flaw that would become legendary in the annals of hacking history. Their presentation exposed a critical error in Sony's implementation of cryptographic algorithms, particularly the Elliptic Curve Digital Signature Algorithm (ECDSA), responsible for creating signatures in the console. What they unveiled wasn't just a minor glitch—it was a seismic vulnerability. By exploiting this flaw, they managed not only to break individual signatures but also to fully recover the private key. This revelation meant that anyone could generate signatures as authentic as Sony's, opening the floodgates to a new era of possibilities.

Although FailOverflow did not disclose the keys during their presentation, renowned hacker George Hotz, also known as Geohot, seized the moment. A few days later, he boldly posted a set of keys on his website, crediting FailOverflow for their pioneering work. This event marked a watershed moment, not only for the PlayStation 3 hacking community but also for the broader understanding of cryptography and system vulnerabilities. In this article, we delve into the intricacies of this remarkable exploit, examining its implications and the enduring impact it has had on digital security.

Understanding PlayStation 3's Security Model

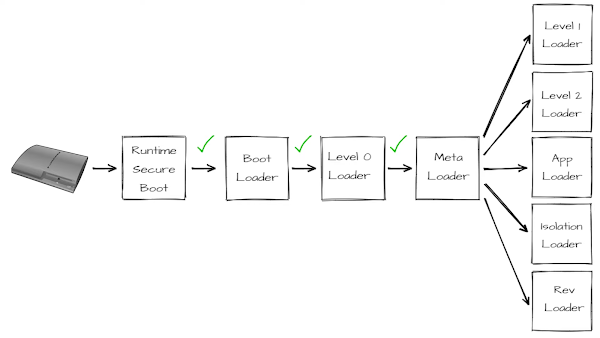
To comprehend the gravity of this flaw, it's crucial to dissect the intricacies of the PlayStation 3's security architecture and delve into the realm of elliptic curve cryptography. The PlayStation 3 operates through a sequence of trust, known as the chain of trust, a hierarchical process fundamental to its security model.

The chain of trust initiates with the secure boot stage, an immutable component etched directly into the hardware. This stage reads and verifies subsequent bootloaders, creating an unbroken chain of verification and execution. Each step in the process relies on the assumption that the preceding step's integrity has not been compromised. For instance, the meta loader, a critical link in this chain, undergoes rigorous integrity checks. Attempting to replace or tamper with it would trigger a failed integrity check, halting the boot process.

The flaw in Sony's implementation lies in their failure to ensure the robustness of these integrity checks. FailOverflow identified a vulnerability that allowed them to circumvent one of these checks without detection. By exploiting this weakness, hackers could modify a crucial link in the chain of trust. This breach allowed unauthorized access to the system's core, giving individuals the power to manipulate the PlayStation 3's software environment without triggering alarms.

Understanding ECDSA

At the core of the PlayStation 3's vulnerability lies the intricate realm of Elliptic Curve Cryptography (ECC), specifically the ECDSA. This cryptographic technique, explored in details in my previous article, is pivotal for verifying data integrity. Unlike symmetric schemes, ECDSA employs an asymmetric approach, involving a private key for creating digital signatures and a corresponding public key for verification (aka Asymmetric Encryption).

To comprehend ECDSA, envision an elliptic curve—a set of points satisfying a specific equation. This curve, defined by the equation

y^2 = x^3+ax+b

, serves as the foundation for cryptographic operations. Here, 'a' and 'b' are parameters, while 'x' and 'y' represent coordinates on the curve. The elegance of ECDSA lies in its peculiar addition method.

When two points P and Q are chosen on the curve, their addition is not the conventional summation of coordinates. Instead, a line is drawn through P and Q, intersecting the curve at a third point. From this intersection, a vertical line is drawn, crossing the curve again. This resulting point, named R, is the outcome of the addition operation. Crucially, this process necessitates an additional point O, often denoted as zero, located infinitely far from the curve—a unique concept vital for the mathematics of elliptic curves.

While visualizing elliptic curves graphically provides an intuitive understanding, cryptography delves into a realm where integers, not smooth lines, matter most. In cryptographic applications, these curves don't always look like the elegant graphs we imagine. Imagine confining ourselves to integers; the curve takes on a jagged appearance, no longer the graceful arch we expect. Moreover, if we restrict calculations to integers from 0 to 36, working modulo 37, the curve becomes an unrecognizable jumble of points.

Here's the intriguing part: despite these seemingly chaotic arrangements, these jagged lines and scattered points still obey the fundamental rules of elliptic curve addition. This means, even if our visual intuition fails us, the mathematical operations still hold true. In the realm of cryptography, it's not about the smoothness of curves; it's about the precise calculations on these jagged, modular lines. This unique quality underlines the elegance of elliptic curve cryptography, where intricate mathematics and computational precision blend to safeguard digital realms, showcasing the beauty of cryptographic algorithms beyond their graphical representations.

In the realm of integers, multiplication involves adding a number to itself multiple times. Similarly, in elliptic curve cryptography, multiplication with a point means repeatedly adding that point to itself as many times as the given integer dictates. For instance, multiplying a point \(p\) by 3 involves adding \(p\) to itself twice, resulting in a new point. This multiplication operation, seemingly simplistic, forms the backbone of intricate cryptographic algorithms, illustrating the unique mathematics that safeguard digital communication.

PlayStation 3 ECDSA Algorithm Parameters

Now, armed with a deeper understanding of elliptic curves, we can unravel the inner workings of the ECDSA algorithm, a pivotal component of the PlayStation 3's cryptographic fortification. In the actual implementation of PS3, specific parameters are paramount. Three colossal numbers, constituting the curve's parameters a, b, and the modulus p, are fundamental. These immense values ensure an astronomical number of points on the curve, bolstering the security.

Crucially, there exists a designated point on this curve known as the generator point G, possessing specific x and y coordinates. Additionally, the parameter n, called the order of G, dictates that if G is added to itself n times (or multiplied by n), it results in the zero point.

Notably, these parameters are not arbitrary; there are standardized sets, like secp256r1 and curve25519, each with unique properties.

These numbers, while integral to the PS3's security, are theoretically public, as the security of ECDSA is ensured by elliptic curve operations, rather than on secrecy. In PS3's specific cases, they are embedded directly into the console's architecture.

The process continues with the creation of a private key d—a secret number known only to Sony. This key, chosen randomly between 1 and n remains securely housed within Sony's headquarters, its confidentiality paramount. Utilizing the multiplication concept described earlier, this private key is multiplied by the generator point G, resulting in a unique point Q on the curve known as the public key.

Remarkably, this public key, while openly available, conceals its origin. If armed with the generator point G and the private key d deriving the public key Q is straightforward. However, the reverse scenario poses an unsolvable puzzle: given Q and G deducing the private key d remains an impossible feat. This cryptographic asymmetry ensures the PS3's security, as unlike conventional multiplication, the origins of these calculated points remain a secret.

Decoding ECDSA Signatures: Ensuring Data Integrity

The intricate process of signing data in ECDSA involves meticulous steps to maintain the integrity of messages. Let's break down this cryptographic dance, starting with the hashing of the data using SHA-1, which turns the message, say "hello world," into a numerical value known as z. To know more about secure hashing, read my previous article.

Next, a crucial step involves generating a random number k followed by a series of calculations. The generator point G is multiplied by k and the resulting x-coordinate is computed modulo n yielding r. If r is zero, the process starts anew. Subsequently, the private key d is multiplied by r and the message z is added to this product. The inverse of k is then applied to this sum, modulo n produces s the second component of the signature - (r,s).

To verify the signature's validity, z is recalculated using the same cryptographic hash function. u1 and u2 are derived from z, r and the inverse of s modulo n.

These values generate a new point on the curve, computed by multiplying u1 with the generator point G and u2 with the public key Q. Adding these points yields a new point, and if its x-coordinate modulo n matches r the signature is valid. This meticulous process ensures the authenticity of digital messages, highlighting the intricate ballet of calculations underpinning ECDSA signatures.

Sony's Fatal Oversight: The Consequence of Reused Secrets

Sony's misstep lay in a seemingly unsuspicious detail: the reuse of a fixed number, k during the signing process. Picture k not as a random variable but a constant value utilized each time a signature was generated. This choice had catastrophic implications, allowing hackers to exploit the flaw and extract the private key, a blunder that reverberated throughout the PlayStation 3's security framework.

Consider two different messages, both signed using the same k value. While r remains consistent, s' and s' (from the two signatures) differ due to the unique nature of the messages. Leveraging these differences, a hacker could derive k using a simple algebraic rearrangement.

With k revealed, the hacker could then reconstruct the private key d. This discovery was nothing short of a goldmine, granting control over the PS3's security apparatus.

By extracting the meta loader and corresponding signatures from different consoles, hackers could apply this flaw methodically. They exploited the predictable k to recover the private key, giving them unprecedented control. With the secret key in hand, they could craft new meta loaders, sign them using the extracted private key, and seize control of any software running after the boot process. This lapse in Sony's security strategy allowed not only the proliferation of pirated games but also facilitated homebrew applications, a significant breach in the PlayStation 3's defense.

Conclusion

The case of the fixed k number serves as a poignant reminder of the critical role randomness plays in cryptographic processes. Sony's oversight, transforming k from a variable into a constant, led to a cascading sequence of events, ultimately unraveling the PS3's fortress-like security and reshaping the gaming landscape. This flaw, a testament to the importance of secure implementation, forever altered the course of digital security in gaming consoles.