Deep dive into Elliptic Curve Signatures

To popular demand, I have decided to try and explain how the ECDSA algorithm works. We've discussed a bit eliptic curve signatures before and a little bit more afte that, but it seems it's never enough.

Admitedly, I've been struggling a bit to understand it properly and while I found a lot of documentation about it, I haven't really found any ECDSA for newbies anywhere. So I thought it would be good to explain in simple terms how it works so others can understand it better.

Let's give it a stab

ECDSA stands for Elliptic Curve Digital Signature Algorithm and it's used to create a digital signature of data (a file for example) in order to allow you to verify its authenticity, without compromising its security. Think of it like a real signature, you can recognize someone's signature, but you can't forge it without others knowing. The ECDSA algorithm is basically all about mathematics. But these maths are fairly complicated, so while I'll try to vulgarize it and make it understandable for non technical people, you will still probably need some knowledge in math to understand it properly. I will do this in two parts, one that is a sort of high level explanation about how it works, and another where I dig deeper into its inner workings to complete your understanding.

The easy part

So the principle is simple, you have a mathematical equation which draws a curve on a graph, and you choose a random point on that curve and consider that your point of origin. Then you generate a random number, this is your private key, you do some magical mathematical equation using that random number and the point of origin and you get a second point on the curve, that's your public key. From the previous article about cryptography basic, we know that if you want to sign a file, you will use this private key (the random number) with a hash of the file (a unique number to represent the file) into a magical equation and that will give you your signature.

R and S

The signature itself is divided into two parts, called R and S. In order to verify that the signature is correct, you only need the public key (that point on the curve that was generated using the private key) and you put that into another magical equation with one part of the signature (S), and if it was signed correctly using the the private key, it will give you the other part of the signature (R). So to make it short, a signature consists of two numbers, R and S, and you use a private key to generate R and S, and if a mathematical equation using the public key and S gives you R, then the signature is valid.

There is no way to know the private key or to create a signature using only the public key.

The heavy part

Let's start with the basics: ECDSA uses only integer mathematics, there are no floating points (this means possible values are 1, 2, 3, etc.. but not 1.5 etc.), also, the range of the numbers is bound by how many bits are used in the signature (more bits means higher numbers, means more security as it becomes harder to guess the critical numbers used in the equation), as you should know, computers use bits to represent data, a bit is a digit in binary notation (0 and 1) and 8 bits represent one byte. Every time you add one bit, the maximum number that can be represented doubles, with 4 bits you can represent values 0 to 15 (for a total of 16 possible values), with 5 bits, you can represent 32 values, with 6 bits, you can represent 64 values, etc. One byte (8 bits) can represent 256 values, and 32 bits can represent 4294967296 values (4 Giga). Usually ECDSA will use 160 bits total, so that makes well, a very huge number with 49 digits in it.

ECDSA is used with a SHA1 cryptographic hash of the message to sign (the file). A hash is simply another mathematical equation that you apply on every byte of data, which will give you a number that is unique to your data. Like for example, the sum of the values of all bytes may be considered a very dumb hash function. So if anything changes in the message (the file) then the hash will be completely different.

In the case of the SHA1 hash algorithm, it will always be 20 bytes (160 bits). It's very useful to validate that a file has not been modified or corrupted, you get the 20 bytes hash for a file of any size, and you can easily recalculate that hash to make sure it matches. What ECDSA signs is actually that hash, so if the data changes, the hash changes, and the signature isn't valid anymore.

Now, how does it work? Well Elliptic Curve cryptography is based on an equation of the form: y^2=(x^3 + a * x + b) mod p. First thing you notice is that there is a modulo and that the y is a square. This means that for any x coordinate, you will have two values of y and that the curve is symmetric on the X axis.

The p is a prime number and makes sure that all the values are within our range of 160 bits. It also allows the use of modular square root and modular multiplicative inverse - mathematics which make calculating stuff easier. Since we have a modulo (p), it means that the possible values of y^2 are between 0 and p-1, which gives us p total possible values. However, since we are dealing with integers, only a smaller subset of those values will be a perfect square (the square value of two integers), which gives us N possible points on the curve where N and p (N being the number of perfect squares between 0 and p).

Since each x will yield two points (positive and negative values of the square-root of y^2), this means that there are N/2 possible x coordinates that are valid and that give a point on the curve. So this elliptic curve has a finite number of points on it, and it's all because of the integer calculations and the modulus.

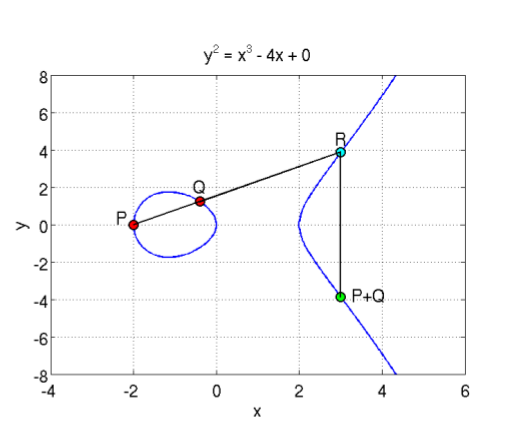
Another thing you need to know about Elliptic curves, is the notion of point addition. It is defined as adding one point P to another point Q will lead to a point S such that if you draw a line from P to Q, it will intersect the curve on a third point R, which is the negative value of S (remember that the curve is symmetric on the X axis). In this case, we define R=-S to represent the symmetrical point of R on the X axis. This is easier to illustrate with an image:

So you can see a curve of the form y^2=x^3 + ax + b (where a=-4 and b=0), which is symmetric on the X axis, and where P+Q is the symmetrical point through X of the point R which is the third intersection of a line going from P to Q. In the same manner, if you do P + P, it will be the symmetrical point of R, which is the intersection of the line that is a tangent to the point P. And P + P + P is the addition between the resulting point of P+P with the point P, since P + P + P can be written as (P+P) + P. This defines the point multiplication, where k*P is the addition of the point P to itself k times.

Here, you can see two elliptic curves, and a point P from, which you draw the tangent, it intersects the curve with a third point, and its symmetric point it 2P, then from there, you draw a line from 2P and P and it will intersect the curve, and the symmetrical point is 3P etc. You can keep doing that for the point multiplication. You can also already guess why you need to take the symmetric point of R, when doing the addition, otherwise, multiple additions of the same point will always give the same line and the same three intersections.

One particularity of this point multiplication is that, if you have a point R=k*P, where you know R and you know P, there is no way to find out what the value of k is. Since there is no point subtraction or point division, you cannot just resolve k=R/P. Also, since you could be doing millions of point additions, you will just end up on another point on the curve, and you'd have no way of knowing how you got there. You can't reverse this operation, and you can't find the value k, which was multiplied with your point P to give you the resulting point R.

This thing where you can't find the multiplicand, even when you know the original and destination points, is the whole basis of the security behind the ECDSA algorithm, and the principle is called a trapdoor function.

Now that we've handled the basics, let's talk about the actual ECDSA signature algorithm. For ECDSA, you first need to know your curve parameters, those are a, b, p, N and G. You already know that a and b are the parameters of the curve function (y^2=x^3 + ax + b), that p is the prime modulus, and that N is the number of points of the curve. But there is also G, that is needed for ECDSA, and it represents a reference point or a point of origin if you prefer. Those curve parameters are important and without knowing them, you obviously can't sign or verify a signature. Yes, verifying a signature isn't just about knowing the public key, you also need to know the curve parameters for which this public key is derived from.

So first of all, you will have a private and a public key. The private key is a random number (of 20 bytes) that is generated, and the public key is a point on the curve generated from the point multiplication of G with the private key. We set dA as the private key (random number) and Qa as the public key (a point), so we have:

Qa=dA * G (where G is the point of reference in the curve parameters)

So how do you sign a file/message?

First, you need to know, that the signature is 40 bytes and is represented by two values of 20 bytes each, the first one is called R and the second one is called S. So the pair (R, S) together is your ECDSA signature. Now here's how you can create those two values in order to sign a file. First you must generate a random value k (of 20 byes), and use point multiplication to calculate the point P=k*G. That point's x value will represent R. Since the point on the curve P is represented by its (x, y) coordinates (each being 20 bytes long), you only need the x value (20 bytes) for the signature, and that value will be called R. Now all you need is the S value.

To calculate S, you must make a SHA1 hash of the message, this gives you a 20 bytes value, that you will consider as a very huge integer number and we'll call it z. Now you can calculate S using the equation:

S=k^-1 (z + dA * R) mod p

Note here the k^-1, which is the modular multiplicative inverse of k - it's basically the inverse of k, but since we are dealing with integer numbers, then that's not possible, so it's a number such that (k^-1 * k) mod p is equal to 1. And again, I remind you that k is the random number used to generate R, z is the hash of the message to sign, dA is the private key and R is the x coordinate of k*G (where G is the point of origin of the curve parameters).

Now that you have your signature, you want to verify it, it's also quite simple, and you only need the public key (and curve parameters of course) to do that. You use this equation to calculate a point P:

P= S^-1*z*G + S^-1 * R * Qa

If the x coordinate of the point P is equal to R, that means that the signature is valid, otherwise it's not. Now let's see why and how and this is going to require some mathematics to verify:

P=S^-1*z*G + S^-1 * R *Qa
// but Qa=dA*G, so:
P=S^-1*z*G + S^-1 * R * dA*G = (S^-1)*(z + dA* R)*G

But the x coordinate of P must match R and R is the x coordinate of k * G, which means that:

k*G=S^-1 (z + dA * R) *G

We can simplify by removing G which gives us:

k=S^-1(z + dA * R)

By inverting k and S, we get :

S=k^-1 (z + dA *R)

And that is the equation used to generate the signature, so it matches, and that is the reason why you can verify the signature with it.

You can note that you need both k (random number) and dA (the private key) in order to calculate S, but you only need R and Qa (public key) to validate the signature. And since R=k*G and Qa=dA*G and because of the trap door function in the ECDSA point multiplication (explained above), we cannot calculate dA or k from knowing Qa and R, this makes the ECDSA a secure algorithm. There is no way of finding the private keys, and there is no way of faking a signature without knowing the private key.

Conclusion

The ECDSA algorithm is used everywhere, and has not been cracked. It is a vital part of most of today's security.

In the context of distributed computing and blockchain technology, ECDSA can play a crucial role in providing a secure and efficient means of verifying transactions on the blockchain.

One potential way that ECDSA could support future innovation in the distributed computing and blockchain ecosystem is by providing a more efficient and secure means of verifying transactions on the blockchain. This could enable the development of new decentralized applications and services that rely on the security and efficiency of ECDSA for their operation.

Another potential benefit of ECDSA is that it can support the development of new, more advanced cryptographic algorithms and protocols. For example, by using ECDSA as a building block, researchers and developers may be able to create new cryptographic techniques that provide even greater security and efficiency than existing algorithms.

Overall, ECDSA has the potential to support a wide range of innovations in the distributed computing and blockchain ecosystem, and its widespread adoption and use will likely play a key role in the continued development and growth of these technologies.