Merkle tree

Have you heard about Merkle trees when discussing blockchain technology? That’s because the Merkle tree is at the core of the technology itself.

What is Merkle Tree

A Merkle tree, also defined as a binary hash tree, is a data structure used to efficiently summarize and validate large data sets. It is a tree structure in which each leaf node is a hash of a block of data, and each non-leaf node is a hash of its children. Typically, Merkle trees have a branching factor of 2, meaning that each node has up to 2 children.

Merkle trees are used in distributed systems for efficient data verification. They are efficient because they use hashes instead of full files. Hashes are ways of encoding files that are much smaller than the actual file itself. Currently, their main uses are in peer-to-peer networks such as Tor, Bitcoin, and Git.

Overview

The Merkle Tree has been all over the place since 1979 when there was a man named Ralph Merkle at Stanford University. Merkle wrote a paper titled “A Certified Digital Signature,” unknowingly creating a significant blockchain component. In his paper, Merkle gave a description of a brand new method of proof-making. Primarily, Merkle designed a data verification process that would allow computers to work much faster than before. Merkle’s idea, now called the Merkle Tree, has fundamentally changed the world of cryptography, including how encrypted computer protocols work. As a result, Merkle Trees has grown in popularity over the years, especially in cryptocurrency. Many cryptocurrencies like Ethereum have also embraced Merkle Trees.

How it works?

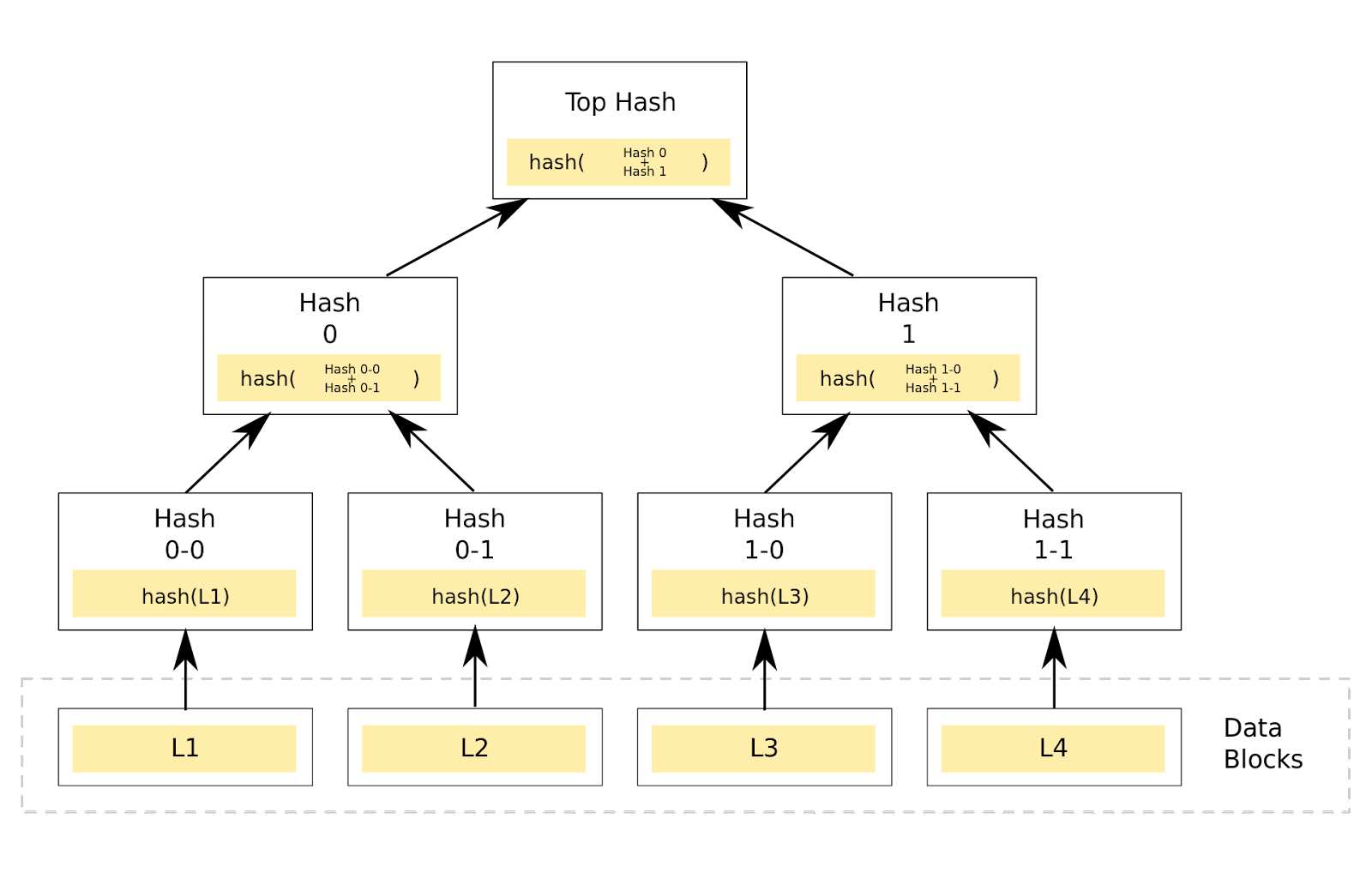
A Merkle tree sums up all transactions in a block by generating a digital fingerprint of the whole set of operations, allowing the user to check whether a transaction is included in a block. Merkle trees are created by repetitively hashing pairs of nodes until only one hash is left, this hash is better called the Merkle Root or the Root Hash. They are constructed from the bottom, from the hashes of individual transactions called Transaction IDs. Thus every leaf node is a hash of transactional data, and each non-leaf node is a hash of its previous hash. Merkle trees are binary and consequently require an equal number of leaf nodes. If the figure of transactions is odd, the last hash will be matched once it creates an even number of leaf nodes. The following image depics the idea:

In this image, we see an input of data broken up into blocks labeled L1 though L4. Each of these blocks are hashed using some hash function. Then each pair of nodes are recursively hashed until we reach the root node, which is a hash of all nodes below it.

Why Merkle Trees are Essential to Blockchain

To grasp how important Merkle Trees are to blockchain technology, imagine a blockchain without them. We’re going to apply to Bitcoin primarily because the usage of Merkle Trees is essential to cryptocurrencies, but also simple to understand. For example, if Bitcoin didn’t have Merkle Trees, every node on the network would need to maintain a full copy of every transaction that has ever happened on Bitcoin. You can imagine how much information it would have been. Any authentication request on Bitcoin would take an incredibly large packet of data to be sent over the network, so you need to have it on your own to verify the data. A computer used for validation would have to use a lot of processing power to compare ledgers to ensure that there were no changes. Merkle Trees fix this problem. They hash records in the accounting, which efficiently segregates the data proof from the data itself. Proving that a transaction is valid only includes giving small amounts of information across the network. Besides, it allows you to demonstrate that both variants of the ledger are the same for titular amounts of computing power and network bandwidth.

Benefits and Protocol

The Merkle tree is useful because it allows users to verify a specific transaction without downloading the whole blockchain. For example, say that you wanted to verify that transaction T, is included in the block L2 in the diagram above. If you have the root hash, the process is like a game of sudoku: you query the network about (Hash 0-1), and it returns (Hash 0-0), (Hash 0), and (Hash 1). The Merkle tree allows you to verify that everything is accounted for with three hashes: given Hash 0-0, Hash 1, and the root, Hash 0-1 (the only missing hash) has to be present in the data.

In various distributed and peer-to-peer systems, data verification is very important. This is because the same data exists in multiple locations. So, if a piece of data is changed in one location, it's important that data is changed everywhere. Data verification is used to make sure data is the same everywhere.

However, it is time-consuming and computationally expensive to check the entirety of each file whenever a system wants to verify data. So, this is why Merkle trees are used. Basically, we want to limit the amount of data being sent over a network (like the Internet) as much as possible. So, instead of sending an entire file over the network, we just send a hash of the file to see if it matches. The protocol goes like this:

• Computer A sends a hash of the file to computer B.
• Computer B checks that hash against the root of the Merkle tree.
• If there is no difference, we're done! Otherwise, go to the next step.
• If there is a difference in a single hash, computer B will request the roots of the two subtrees of that hash.
• Computer A creates the necessary hashes and sends them back to computer B.
• Repeat steps 4 and 5 until you've found the data blocks(s) that are inconsistent. It's possible to find more than one data block that is wrong because there might be more than one error in the data.
• Note that each time a hash is found to match, we need nn more comparisons at the next level, where nn is the branching factor of the tree.

Conclusion

Once you understand the fundamentals of Merkle Trees, you can begin to appreciate the protection and efficiency of Blockchain data structures. In all probability, if Merkle Trees had never been discovered, cryptocurrency and blockchain technology would never have existed. Unless there was a suitable alternative, the amount of computing power and storage would be too costly to operate. Merkel Trees are vital to blockchains and allow them to function while maintaining transaction integrity.