Practical Byzantine Fault Tolerance (pBFT)

Blockchain technology represents a sum of many parts, and its consensus algorithm is certainly one of the most important pieces of this puzzle. Decentralized blockchains are envisioned as peer-to-peer systems that don’t have centralized authority points; consensus algorithms play a massive role in enabling this decentralized infrastructure to exist and work.

Typical centralized systems rely on trust where certain entities act as network “leaders”, controlling the network and making important decisions about it.

Everyone else trusts these leaders that they’ll stay honest and behave in a manner beneficial to the entire network. This can sometimes backfire as the network leaders can become corrupt and start acting in malicious ways. When this happens, the entire network is put at risk.

By basing decentralized blockchain networks on a consensus (which is achieved between a network of widely distributed nodes that manage the blockchain), original programmers of cryptocurrencies like Bitcoin introduced a dynamic, non-centrally-controlled way of reaching agreement in a group.

This gave decentralized blockchains the ability to stay immutable, censorship-free, central-point-of-failure-free and infinitely more secure than similar centralized data management systems.

The Byzantine Fault Tolerance problem

A problem with governing decentralized data aggregating blockchains via consensus comes when the nodes that are a part of the consensus become faulty or malicious.

A node can start disobeying the network rules and start presenting fake data to other nodes. The question that arises here is the following: how will the honest nodes acknowledge that this data is fake and come to a consensus about not adding it to the blockchain?

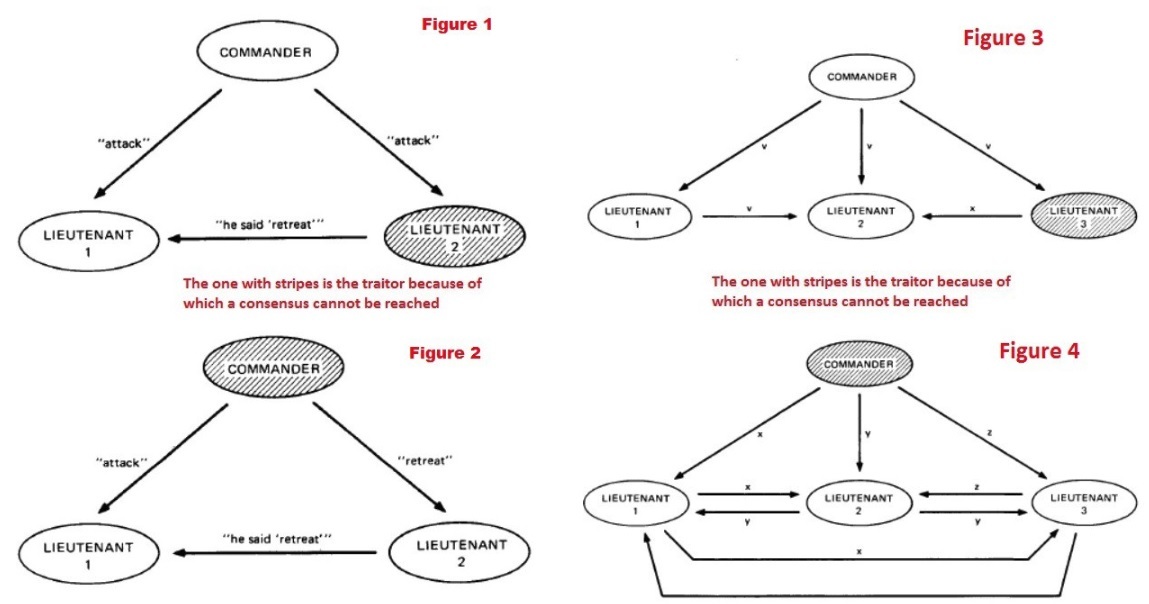
This problem is known in the literature as a Byzantine Fault Tolerance Problem. BFT problem is seen as a generalized version of the Two Generals Problem that adds a twist of having more than two generals in the mix to the story. The Two Generals Problem presents us with a hypothetical scenario where two Byzantine generals, one being the superior to the other, are sitting on the opposite walls of an enemy city they are trying to conquer.

Each general’s army on its own is not enough to take over the city successfully, which is why they need to coordinate a joint attack that will happen at an exact time.

The issue becomes apparent when the attack coordination starts; the superior general has to send a messenger through the sieged city to inform the second general that the attack will happen at a determined time. The messenger can deliver the time of attack successfully to the other general but he can also easily get caught by the enemy.

The enemy now knows the exact time of the attack and can even send a fake message to the second general, duping him into attacking earlier/later or into staying put. The second general now has to send a messenger back to the first one, confirming that he received the instructions. This messenger can also be captured and his message altered, leading to a situation where it’s impossible for the generals to reach an agreement.

BFT problem, as explained before, adds more than two generals that need to agree on a time to attack an enemy city. Interestingly enough in this case there is a potential solution, as the goal isn’t to have all the generals attack at the same time but rather to have a majority of them do so. If more than two thirds of generals listen to the supreme commander and attack at the same time, the city will be taken. The problem can be presented as follows:

When transferred to blockchain, each node is basically one of the generals from the story. One node will provide data that the others will need to come to a consensus regarding whether or not this data should be added to the blockchain.

If more than two thirds of network nodes are capable of reaching a consensus that stays true to the pre-determined rules of the decentralized blockchain, the consensus algorithm is considered as Byzantine Fault-tolerant.

Practical Byzantine Fault Tolerance

Practical Byzantine Fault Tolerance is a consensus algorithm introduced in the late 90s by Barbara Liskov and Miguel Castro. pBFT was designed to work efficiently in asynchronous(no upper bound on when the response to the request will be received) systems. It is optimized for low overhead time. Its goal was to solve many problems associated with already available Byzantine Fault Tolerance solutions.

pBFT consensus algorithm allows a distributed system to reach a consensus even when a small amount of nodes demonstrate malicious behavior (such as falsifying information). During information transmission, pBFT uses cryptographic algorithms such as signature, signature verification, and hash to ensure that everything stays irrevocable, unforgeable, and indisputable. It also optimizes the BFT algorithm, reducing its complexity from exponential to polynomial. In a distributed system that constitutes 3f+1 nodes (f represents the number of byzantine nodes), a consensus can be reached as long as no less than 2f+1 (or 66%) non-byzantine nodes are functioning normally.

How it works

pBFT consensus consists of three phases: Pre-Prepare, Prepare, and Commit. Together, they form the core of the pBFT consensus algorithm:

• Pre-Prepare: Primary node is responsible for verifying the requests and generating corresponding pre-prepare messages. Then, the Primary node will broadcast pre-prepare messages to all Replica nodes. After receiving the messages, Replica nodes will verify the legitimacy of those pre-prepare messages and then broadcast a corresponding prepare message.
• Prepare: Gathering prepare messages. After a certain node gathers 2f+1 prepare messages, it will announce that it is ready for block submission and start to broadcast commit messages;
• Commit: Gathering commit messages. After a certain node gathers 2f+1 commit messages, it will process the native requests cached locally and make corresponding changes to the system state.

The algorithm is quite message-heavy, as nodes (also known as replicas) need to inform every other replica on the network of their decision.

One pBFT algorithm needs to have a minimum of 3f + 1 replicas (where f is the maximum number of faulty replicas) to ensure that its Byzantine Fault tolerance is unharmed. For example, a system with 7 replicas (presumption being that 2 of those are faulty) would need to exchange 71 messages to achieve consensus, while increasing the number of faulty replicas by one would increase the number of required replicas to 10 and the number of required messages to 142.

Nodes in a pBFT enabled distributed system are sequentially ordered with one node being the primary (so-called leader node) and others considered as secondary (the backup nodes). Any node in the system can assume the role of primary if an old primary node fails or starts acting maliciously. The primary node is changed during every consensus round nonetheless.

View change

View-change protocol is crucial to pBFT consensus algorithm. When there’s no consensus on a request in a limited time, the old data maintains consistency, and the system keeps the current status. To fulfill systematic availability, pBFT consensus algorithm applies the view-change protocol to render the system available again. When the view-change protocol is executed, a new Primary node will be elected to strike a consensus and respond to client in a limited time, so as to fulfill the availability requirement.

The core reason for triggering the view-change protocol is that the Replica node confirms that in limited time, the current Primary node cannot reach a consensus on the exchange request. It may be because the Primary node is temporarily unavailable or it’s a fault node, or the network is unstable for the current distributed system, etc. View-change protocol needs to take into account multiple possibilities to realize tolerance for Byzantine nodes. For example, Byzantine nodes might trigger the view-change protocol, and the Primary node might be a Byzantine node in the new view, which is a topic by itself. It should be noted that the view change will not roll back a commit message. In other words, a consensus in the old view (n) is still valid in the new view.

pBFT Pros and Cons

Pros

pBFT consensus algorithm tolerates faults of a certain number of Byzantine nodes to provide safety and activity for an asynchronous distributed system. Improving on the BFT (Byzantine Fault Tolerance), pBFT algorithm lowers the systematic complexity from the exponential level to the polynomial level, so that BFT is applicable to real systems. PBFT consensus mechanism guarantees that the distributed system offers strong consistency. It is fit for scenarios on private and alliance chains.

Cons

pBFT features complex communication and low scalability. When the number of consensus nodes in the distributed system is large enough, the functionality will go down dramatically. When there’s a great deal of network partition, consensus efficiency will be compromised and result in a huge delay.

Optimizations to pBFT

We cannot reduce the number of messages with pBFT, so that leaves us with reducing the required cryptographic proof needed for the messages. MACs are orders of magnitude less CPU intensive than RSA digital signatures For this reason RSA digital signatures are only used for the view change and new-view messages, which are only sent to promote a backup replica to a primary replica. View changes only happen after a primary has become faulty or k requests have been processed. All other messages are authenticated using MACs like SHA256.

Summary

Unlike PoW or PoS (Proof of Stake) mechanisms, pBFT doesn’t require any hashing power to add new blocks to the underlying blockchain. This makes the algorithm much more energy efficient and eventually allows it to avoid issues with centralization that PoW (mining pools) and PoS (large stake holders cutting deals behind the scenes) suffer from.